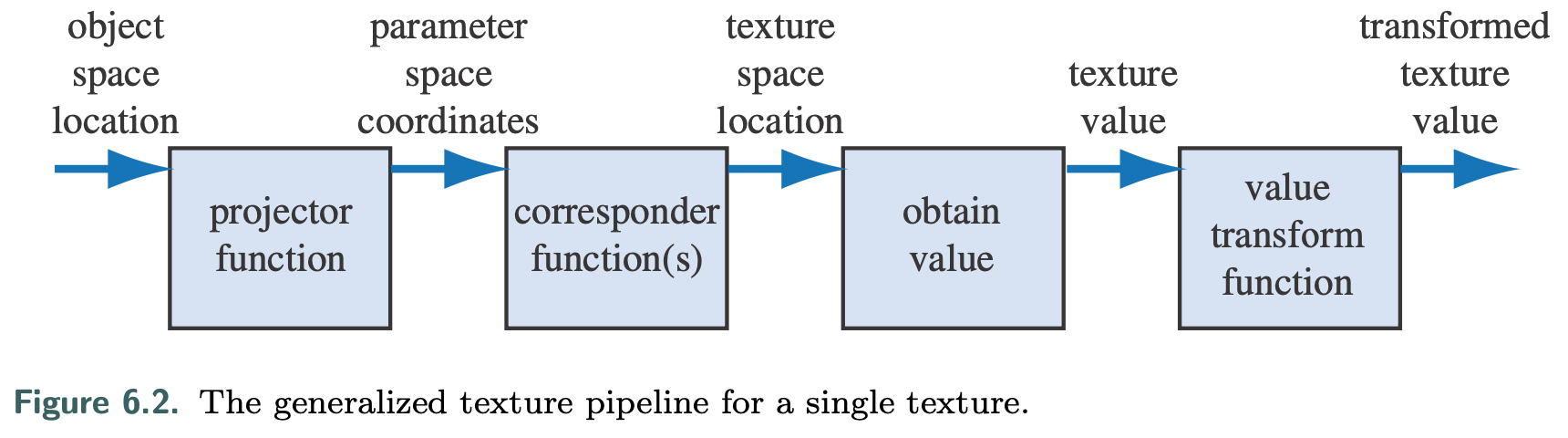
The Texturing Pipeline
Texturing is a technique for efficiently modeling variations in a surface’s material and finish. Texturing works by modifying the values used in the shading equation. The pixels in the image texture are often called texels, to differentiate them from the pixels on the screen.
Texturing can be described by a generalized texture pipeline.
- Object space location A location in space is the starting point for the texturing process. This location can be in world space, but is more often in the model’s frame of reference, so that as the model moves, the texture moves along with it.
- Parameter space coordinates this point in space then has a projector function applied to it to obtain a set of numbers, called texture coordinates, that will be used for accessing the texture. This process is called mapping, which leads to the phrase texture mapping.
- Texture space location Before these new values may be used to access the texture, one or more corre- sponder functions can be used to transform the texture coordinates to texture space. These texture-space locations are used to obtain values from the texture.
- Texture value The retrieved values are then potentially transformed yet again by a value transform function, and finally these new values are used to modify some property of the surface
- Transformed texture value
The reason for the complexity of the pipeline is that each step provides the user with a useful control. It should be noted that not all steps need to be activated at all times.
The Projector Function
The first step in the texture process is obtaining the surface’s location and projecting it into texture coordinate space, usually two-dimensional (u,v) space.
Projector functions typically work by converting a three-dimensional point in space into texture coordinates. Functions commonly used in modeling programs include spherical, cylindrical, and planar projections.
Other inputs can be used to a projector function.
- the surface normal can be used to choose which of six planar projection directions is used for the surface.
- Problems in matching textures occur at the seams where the faces meet, which could be blended.
- polycube maps, where a model is mapped to a set of cube projections, with different volumes of space mapping to different cubes.
Other projector functions are not projections at all, but are an implicit part of surface creation and tessellation.
- parametric curved surfaces have a natural set of (u,v) values as part of their definition.
- The texture coordinates could also be generated from all sorts of different parameters, such as the view direction, temperature of the surface, or anything else imaginable.
Non-interactive renderers often call these projector functions as part of the rendering process itself. In real-time work, projector functions are usually applied at the modeling stage, and the results of the projection are stored at the vertices.
sometimes it is advantageous to apply the projection function in the vertex or pixel shader. Doing so can increase precision, and helps enable various effects, including animation (Section 6.4).
Some rendering methods, such as environment mapping(Section 10.4), have specialized projector functions of their own that are evaluated per pixel.
As there is severe distortion for surfaces that are edge-on to the projection direction, the artist often must manually decompose the model into near-planar pieces. There are also tools that help minimize distortion by unwrapping the mesh, or creating a near-optimal set of planar projections.
The goal is to have each polygon be given a fairer share of a texture’s area, while also maintaining as much mesh connectivity as possible. Connectivity is important in that sampling artifacts can appear along edges where separate parts of a texture meet.
Section 16.2.1 discusses how texture distortion can adversely affect rendering. This unwrapping process is one facet of a larger field of study, mesh parameterization.
The texture coordinate space is not always a two-dimensional plane; sometimes it is a three-dimensional volume. In this case, the texture coordinates are presented as a three-element vector, (u,v,w), with w being depth along the projection direction. Other systems use up to four coordinates, often designated (s, t, r, q); q is used as the fourth value in a homogeneous coordinate. It acts like a movie or slide projector, with the size of the projected texture increasing with distance.
Another important type of texture coordinate space is directional, where each point in the space is accessed by an input direction. One way to visualize such a space is as points on a unit sphere, the normal at each point representing the direction used to access the texture at that location. The most common type of texture using a directional parameterization is the cube map (Section 6.2.4).
It is also worth noting that one-dimensional texture images and functions have their uses. For example, on a terrain model the coloration can be determined by altitude, e.g., the lowlands are green; the mountain peaks are white. Lines can also be textured; one use of this is to render rain as a set of long lines textured with a semitransparent image. Such textures are also useful for converting from one value to another, i.e., as a lookup table.
Since multiple textures can be applied to a surface, multiple sets of texture coordinates may need to be defined. However the coordinate values are applied, the idea is the same: These texture coordinates are interpolated across the surface and used to retrieve texture values. Before being interpolated, however, these texture coordinates are transformed by corresponder functions.
The Corresponder Function
Corresponder functions convert texture coordinates to texture-space locations. They provide flexibility in applying textures to surfaces.
Another class of corresponder functions controls the way an image is applied. We know that an image will appear on the surface where (u, v) are in the [0, 1] range. But what happens outside of this range? Corresponder functions determine the behavior. In OpenGL, this type of corresponder function is called the “wrapping mode”; in DirectX, it is called the “texture addressing mode.” Common corresponder functions of this type are:
- wrap (DirectX), repeat (OpenGL), or tile—The image repeats itself across the surface; algorithmically, the integer part of the texture coordinates is dropped. This function is useful for having an image of a material repeatedly cover a surface, and is often the default.
- mirror—The image repeats itself across the surface, but is mirrored (flipped) on every other repetition. For example, the image appears normally going from 0 to 1, then is reversed between 1 and 2, then is normal between 2 and 3, then is reversed, and so on. This provides some continuity along the edges of the texture.
- clamp (DirectX) or clamp to edge (OpenGL)—Values outside the range [0, 1] are clamped to this range. This results in the repetition of the edges of the image texture. This function is useful for avoiding accidentally taking samples from the opposite edge of a texture when bilinear interpolation happens near a texture’s edge.**
- **border (DirectX) or clamp to border (OpenGL)—Texture coordinates out- side [0, 1] are rendered with a separately defined border color. This function can be good for rendering decals onto single-color surfaces, for example, as the edge of the texture will blend smoothly with the border color.
Repeated tiling of a texture is an inexpensive way of adding more visual detail to a scene. However, this technique often looks unconvincing after about three repetitions of the texture, as the eye picks out the pattern. A common solution to avoid such periodicity problems is to combine the texture values with another, non-tiled, tex- ture.
Another option to avoid periodicity is to use shader programs to implement specialized corresponder functions that randomly recombine texture patterns or tiles.