Irregular Z-buffer Shadows
Shadow-map approaches of various sorts are popular for several reasons. Their costs are predictable and scale well to increasing scene sizes, at worst linear with the number of primitives. They map nicely onto the GPU, as they rely on rasterization to regularly sample the light’s view of the world. However, due to this discrete sampling, problems arise because the locations the eye sees do not map one-to-one with those the light sees. Various aliasing problems arise when the light samples a surface less frequently than the eye. Even when sampling rates are comparable, there are biasing problems because the surface is sampled in locations slightly different than those the eye sees.
Shadow volumes provide an exact, analytical solution, as the light’s interactions with surfaces result in sets of triangles defining whether any given location is lit or in shadow. The unpredictable cost of the algorithm when implemented on the GPU is a serious drawback. The improvements explored in recent years are tantalizing, but have not yet had an “existence proof” of being adopted in commercial applications.
Another analytical shadow-testing method may have potential in the longer term: ray tracing. Described in detail in Section 11.2.2, the basic idea is simple enough, especially for shadowing. A ray is shot from the receiver location to the light. If any object is found that blocks the ray, the receiver is in shadow. Much of a fast ray tracer’s code is dedicated to generating and using hierarchical data structures to minimize the number of object tests needed per ray. Building and updating these structures each frame for a dynamic scene is a decades-old topic and a continuing area of research.
Another approach is to use the GPU’s rasterization hardware to view the scene, but instead of just z-depths, additional information is stored about the edges of the occluders in each grid cell of the light . For example, imagine storing at each shadow-map texel a list of triangles that overlap the grid cell. Such a list can be generated by conservative rasterization, in which a triangle generates a fragment if any part of the triangle overlaps a pixel, not just the pixel’s center (Section 23.1.2). One problem with such schemes is that the amount of data per texel normally needs to be limited, which in turn can lead to inaccuracies in determining the status of every receiver location. Given modern linked-list principles for GPUs , it is certainly possible to store more data per pixel. However, aside from physical memory limits, a problem with storing a variable amount of data in a list per texel is that GPU processing can become extremely inefficient, as a single warp can have a few fragment threads that need to retrieve and process many items, while the rest of the threads are idle, having no work to do. Structuring a shader to avoid thread divergence due to dynamic “if” statements and loops is critical for performance.
An alternative to storing triangles or other data in the shadow map and testing receiver locations against them is to flip the problem, storing receiver locations and then testing triangles against each. This concept of saving the receiver locations, first explored by Johnson et al. and Aila and Laine , is called the irregular z-buffer (IZB). The name is slightly misleading, in that the buffer itself has a normal, regular shape for a shadow map. Rather, the buffer’s contents are irregular, as each shadowmap texel will have one or more receiver locations stored in it, or possibly none at all.
Using the method presented by Sintorn et al. and Wyman et al. , a multi-pass algorithm creates the IZB and tests its contents for visibility from the light. First, the scene is rendered from the eye, to find the z-depths of the surfaces seen from the eye. These points are transformed to the light’s view of the scene, and tight bounds are formed from this set for the light’s frustum. The points are then deposited in the light’s IZB, each placed into a list at its corresponding texel. Note that some lists may be empty, a volume of space that the light views but that has no surfaces seen by the eye. Occluders are conservatively rasterized to the light’s IZB to determine whether any points are hidden, and so in shadow. Conservative rasterization ensures that, even if a triangle does not cover the center of a light texel, it will be tested against points it may overlap nonetheless.
Visibility testing occurs in the pixel shader. The test itself can be visualized as a form of ray tracing. A ray is generated from an image point’s location to the light. If a point is inside the triangle and more distant than the triangle’s plane, it is hidden. Once all occluders are rasterized, the light-visibility results are used to shade the surface. This testing is also called frustum tracing, as the triangle can be thought of as defining a view frustum that checks points for inclusion in its volume.
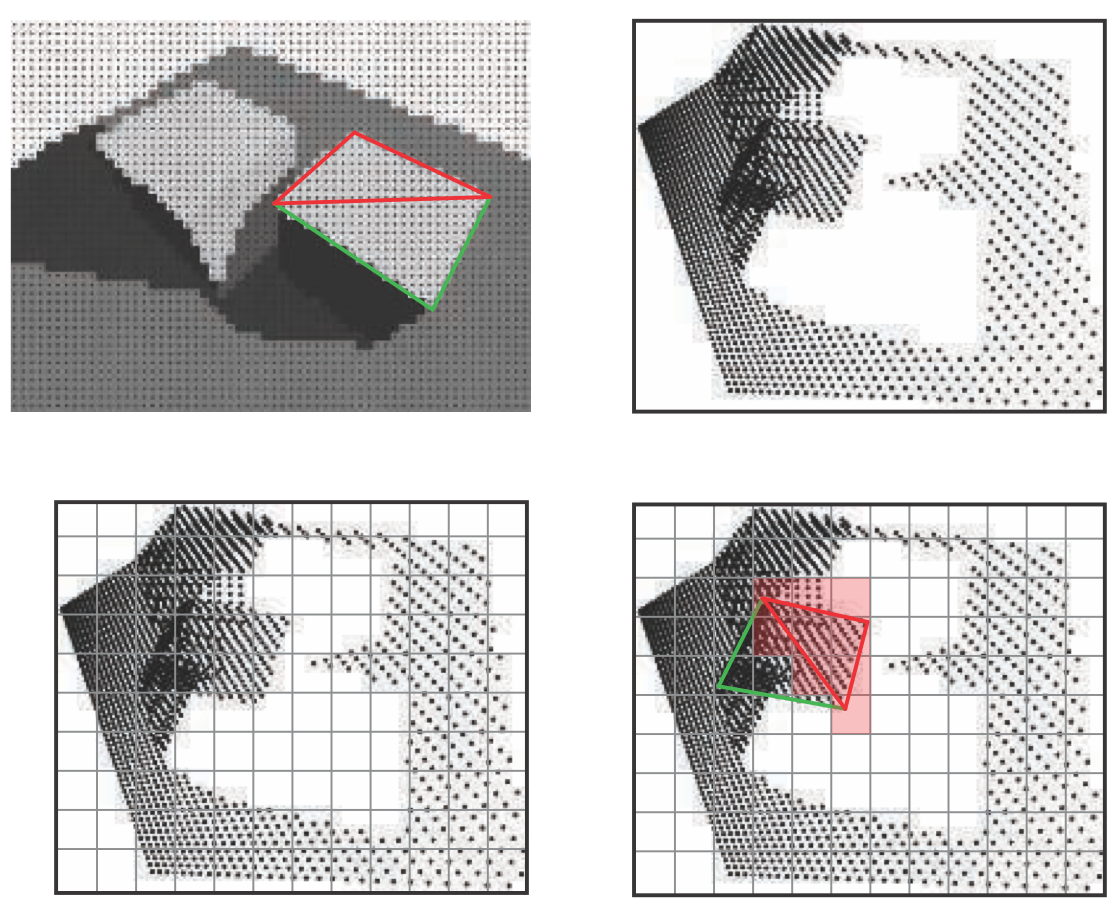
Irregular z-buffer. In the upper left, the view from the eye generates a set of dots at the pixel centers. Two triangles forming a cube face are shown. In the upper right, these dots are shown from the light’s view. In the lower left, a shadow-map grid is imposed. For each texel a list of all dots inside its grid cell is generated. In the lower right, shadow testing is performed for the red triangle by conservatively rasterizing it. At each texel touched, shown in light red, all dots in its list are tested against the triangle for visibility by the light.
Careful coding is critical in making this approach work well with the GPU. Wyman et al. note that their final version was two orders of magnitude faster than the initial prototypes. Part of this performance increase was straightforward algorithm improvements, such as culling image points where the surface normal was facing away from the light (and so always unlit) and avoiding having fragments generated for empty texels. Other performance gains were from improving data structures for the GPU, and from minimizing thread divergence by working to have short, similar-length lists of points in each texel. Figure 7.30 shows a low-resolution shadow map with long lists for illustrative purposes. The ideal is one image point per list. A higher resolution gives shorter lists, but also increases the number of fragments generated by occluders for evaluation.
As can be seen in the lower left image in Figure 7.30, the density of visible points on the ground plane is considerably higher on the left side than the right, due to the perspective effect. Using cascaded shadow maps helps lower list sizes in these areas by focusing more light-map resolution closer to the eye.
This approach avoids the sampling and bias issues of other approaches and provides perfectly sharp shadows. For aesthetic and perceptual reasons, soft shadows are often desired, but can have bias problems with nearby occluders, such as Peter Panning. Story and Wyman explore hybrid shadow techniques. The core idea is to use the occluder distance to blend IZB and PCSS shadows, using the hard shadow result when the occluder is close and soft when more distant. See Figure 7.31. Shadow quality is often most important for nearby objects, so IZB costs can be reduced by using this technique on only a selected subset. This solution has successfully been used in video games.
On the left, PCF gives uniformly softened shadows for all objects. In the middle, PCSS softens the shadow with distance to the occluder, but the tree branch shadow overlapping the left corner of the crate creates artifacts. On the right, sharp shadows from IZB blended with soft from PCSS give an improved result.